 กฎเบื้องต้นเกี่ยวกับการนับ
กฎเบื้องต้นเกี่ยวกับการนับ
ถ้าให้ S เป็นแซมเปิลสเปซ และ A เป็นเหตุการณ์
ใดๆจากการทดลองสุ่ม แล้ว
ตัวแปรสุ่ม ( Random Variable )
ตัวแปรสุ่ม คือ ตัวแปร ซึ่งค่าของตัวแปรดังกล่าวนี้จะถูก
กำหนดโดยผลลัพธ์จากการทดลองเชิงสุ่ม
ตัวแปรสุ่มแบ่งออกเป็น 2 ประเภท ดังนี้
ตัวแปรสุ่มแบบไม่ต่อเนื่อง ( Discrete random variable )
ตัวแปรสุ่มแบบต่อเนื่อง ( Continuous random variable )
การแจกแจงความน่าจะเป็นของตัวแปรสุ่มแบบไม่ต่อเนื่อง ( Discrete Probability Distribution
ฟังก์ชันความน่าจะเป็นของตัวแปรสุ่มแบบไม่ต่อเนื่อง
ถ้า X เป็นตัวแปรสุ่มไม่ต่อเนื่อง โดยที่ X มีค่าเป็นที่
เป็นไปได้ คือ x1, x2, x3,…,xn ฟังก์ชันความน่าจะเป็นที่
X จะมีค่าใดๆ แทนด้วย P(X) = P(X=x) = f(X)
โดยฟังก์ชันความน่าจะเป็นของ X มีคุณสมบัติดังต่อไปนี้
1. ความน่าจะเป็นของตัวแปรสุ่ม X ต้องมีค่าอยู่ในช่วง ศูนย์ถึงหนึ่ง
2. ผลรวมของการแจกแจงความน่าจะเป็นของตัวแปรสุ่ม X มีค่าเท่ากับ 1
การแจกแจงความน่าจะเป็นแบบทวินาม
( Binomial Distribution )
( Binomial Distribution )
การทดลองที่ประกอบไปด้วยการทดลองย่อยที่เป็นอิสระกัน n
ครั้ง โดยที่ผลลัพธ์ของการทดลองย่อยแต่ละครั้งมี 2 อย่าง คือ
สำเร็จ และไม่สำเร็จ ซึ่งถ้ากำหนดให้ความน่าจะเป็นที่จะได้
ผลลัพธ์ คือ ความสำเร็จ มีค่าเท่ากับ p เพราะฉะนั้น ความน่าจะ
เป็นที่จะได้ผลลัพธ์ คือ ความไม่สำเร็จ จะมีค่าเท่ากับ 1-p = q
ถ้ากำหนดให้ X เป็นตัวแปรสุ่ม แทนจำนวนครั้งที่เกิดความ
สำเร็จ ดังนั้นค่าที่เป็นได้ของ X คือ X = 0, 1, 2, 3,…,n
X จะมีค่าเฉลี่ย
และความแปรปรวน
ตัวอย่าง
ร้านขายหลอดไฟแห่งหนึ่งทราบว่าในกล่องใบหนึ่งมี
หลอดไฟจำนวน 8 หลอด ถ้าความน่าจะเป็นที่จะพบหลอด
ไฟเสียเท่ากับ 0.35 จงหาความน่าจะเป็น
1. หลอดไฟเสีย 3 หลอด
2. หลอดไฟเสียไม่เกิน 1 หลอด
3. จงหาค่าเฉลี่ย และความแปรปรวน ของจำนวนหลอดไฟเสีย
การแจกแจงความน่าจะเป็นแบบปัวส์ซอง
( Poisson Distribution )
( Poisson Distribution )
การแจกแจงความน่าจะเป็นแบบปัวส์ซองเป็นการศึกษาความ
น่าจะเป็นของตัวแปรสุ่มที่ถูกกำหนดจากเหตุการณ์ที่เกิดขึ้นในช่วง
เวลาหนึ่งหรือขอบเขตหนึ่งที่สนใจ ซึ่ง l เป็นจำนวนครั้งของ
ความสำเร็จที่เกิดขึ้นโดยเฉลี่ย ( l > 0 )
ถ้ากำหนดให้ X เป็นตัวแปรสุ่มแทนจำนวนครั้งที่ให้ผลสำเร็จใน
ช่วงเวลาหนึ่งหรือขอบเขตหนึ่ง ค่าที่เป็นไปได้ของ X มีค่าดังต่อไป
นี้ X = 0, 1, 2, 3,…,n
ฟังก์ชันการแจกแจงความน่าจะเป็นของ X คือ

X จะมีค่าเฉลี่ย
และความแปรปรวน
ตัวอย่าง
ในหน้าหนังสือพิมพ์หนึ่งหน้า โดยเฉลี่ยมีคำที่พิมพ์ผิด 5
คำ ถ้า นาย ก. อ่านหนังสือพิมพ์ฉบับนี้
จงหาความน่าจะเป็น
1. มีคำที่พิมพ์ผิด 3 คำ
2. มีคำที่พิมพ์ผิดไม่เกิน 1 คำ
3. จงหาค่าเฉลี่ยและความแปรปรวนของคำที่พิมพ์ผิด
การแจกแจงความน่าจะเป็นต่อเนื่อง
( Continuous Probability Distribution
ฟังก์ชันความหนาแน่นของตัวแปรสุ่มแบบต่อเนื่อง
ถ้า X เป็นตัวแปรสุ่มต่อเนื่อง โดยที่ฟังก์ชัน
ความหนาแน่นของ X จะมีค่าใดๆ แทนด้วย f(X)
และ ความน่าจะเป็นของเหตุการณ์ A คือ


1. ความน่าจะเป็นของตัวแปรสุ่ม X ต้องมีค่าอยู่ในช่วง ศูนย์ถึงหนึ่ง
2. พื้นที่ใต้เส้นโค้งการแจกแจงความน่าจะเป็นของตัวแปรสุ่ม X มีค่าเท่ากับ 1
การแจกแจงปกติ ( Normal Distribution )
ถ้าตัวแปรสุ่ม X มีการแจกแจงปกติ
ฟังก์ชันความหนาแน่นของความน่าจะเป็นของ X คือ
โดยที่

การแปลงจากตัวแปรสุ่ม X ที่มีการแจกแจงแบบปกติที่
มีค่าเฉลี่ย m และความแปรปรวน s2 ไปเป็นตัวแปรสุ่ม
Z ที่มีการแจกแจงแบบปกติมาตรฐานที่มีค่าเฉลี่ยเป็น 0
และความแปรปรวนเท่ากับ 1 โดยที่
การคำนวณหาค่าความน่าจะเป็นของตัวแปรสุ่มที่มีการ
แจกแจงแบบปกติ
1. แปลงตัวแปรสุ่ม X ให้เป็นตัวแปรสุ่ม Z โดยที่





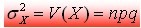













ไม่มีความคิดเห็น:
แสดงความคิดเห็น